首先，什么是平面连通图?

平面连通图是一个二维网络,网络由节点和边组成,比如我随手画了一个:

其次，欧拉公式是沃特?

欧拉公式也叫欧拉定理,指在简单多面体上，棱数（边）、面数和点数具有一定的关系：点+面=边+2。而且规定,平面网络属于特殊的一种多面体,想不到吧（关于欧拉定理的详解，请转向我的另一篇论文《浅谈欧拉定理》），这里要注意一下，数面数的时候要算上整个图外侧的那个无穷大的面，也就是环路的数量加上1。因此平面连通图恒满足欧拉定理。   至于我为什么要介绍欧拉公式呢，是为了做准备，后面的最小生成树需要用到它！

然后，生成树有啥特点？

在平面连通图中，我们想要用一个如树枝一般层层分岔但无环的线路经过所有的节点，且这个线路必须被包含于连通图。换个说法就是，在这个连通图中，我们希望删除掉一些边，让剩下所有的边都没有形成环，且剩下的边必须相互连通，不能被隔绝，这就是生成树（spanning tree）。比如这样：

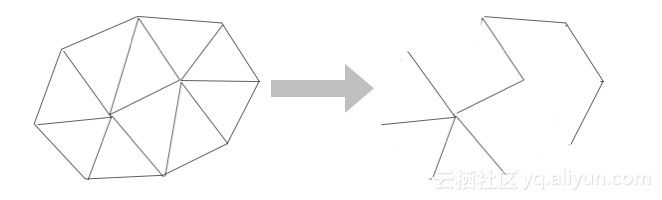
可以看出，不同的删边方法可以得到不同的生成树。   根据欧拉公式，生成树中的面数为1，点数不变还是n，因而得到边数等于n-1，对于连通图中的所有生成树都成立。   还是根据欧拉公式可以证明，此时在生成树中随便增添一条边（这条边当然要属于原连通图中），都必然将多出一个环，增加n条边就产生n个环。   把这张连通图看成一张地图，每个节点都是一个地点，每条边都是可走的路径，这时给每条路径赋予一个权重值，代表这条路径的长短，这在TCP/IP协议中叫做度量值或开销（cost），所以这里权值越大，路径开销反而越大。   因此，不同的生成树的总开销未必相同，其中总开销最小的就成为了本文探讨的最小生成树。   还可以看出，在树上，任意两点之间走的路径是最短距离（放之于原来的连通图比较来说）的可能性很小。所以最小生成树不是地图上寻路的最好方法。

之后，求最小生成树的两种重要算法

以上都是最基础的铺垫部分，写教程就这点麻烦，一定要从知识的根源开始讲起。那么废话不再多说，直接上算法：kruskal（克鲁斯卡尔）算法和prim（普利木）算法。这两个算法是计算最小生成树最常用的算法没有之一，因为他们既简单又完美，况且他们有很多的相似之处。

Kruskal Algorithm

前期准备：